A Car in Stop and go Traffic Starts at Rest Moves Forward 25 M in 8 0 S Then Comes to Rest Again

Learning Objectives

Past the terminate of this section, you volition be able to:

• Identify which equations of movement are to be used to solve for unknowns.
• Use advisable equations of motion to solve a ii-body pursuit problem.

You might guess that the greater the dispatch of, say, a car moving abroad from a terminate sign, the greater the car's deportation in a given time. But, we accept not developed a specific equation that relates dispatch and displacement. In this section, we look at some convenient equations for kinematic relationships, starting from the definitions of displacement, velocity, and dispatch. We first investigate a single object in motion, chosen single-trunk motion. And then we investigate the move of ii objects, called two-trunk pursuit problems.

Note

First, let us make some simplifications in notation. Taking the initial fourth dimension to be nix, as if time is measured with a stopwatch, is a not bad simplification. Since elapsed fourth dimension is [latex] \text{Δ}t={t}_{\text{f}}-{t}_{0} [/latex], taking [latex] {t}_{0}=0 [/latex] means that[latex] \text{Δ}t={t}_{\text{f}} [/latex], the terminal time on the stopwatch. When initial fourth dimension is taken to be zero, we utilize the subscript 0 to announce initial values of position and velocity. That is, [latex] {10}_{0} [/latex] is the initial position and [latex] {v}_{0} [/latex] is the initial velocity. We put no subscripts on the final values. That is, t is the final time, x is the final position, and v is the final velocity. This gives a simpler expression for elapsed time, [latex] \text{Δ}t=t [/latex]. Information technology also simplifies the expression for x deportation, which is now [latex] \text{Δ}x=x-{x}_{0} [/latex]. Also, it simplifies the expression for change in velocity, which is now [latex] \text{Δ}five=v-{5}_{0} [/latex]. To summarize, using the simplified annotation, with the initial time taken to be zero,

[latex] \begin{array}{c}\text{Δ}t=t\hfill \\ \text{Δ}ten=x-{x}_{0}\hfill \\ \text{Δ}v=v-{5}_{0},\hfill \end{array} [/latex]

where the subscript 0 denotes an initial value and the absence of a subscript denotes a final value in whatever motion is under consideration.

We now make the important assumption that acceleration is constant. This assumption allows united states of america to avoid using calculus to find instantaneous acceleration. Since dispatch is constant, the average and instantaneous accelerations are equal—that is,

[latex] \overset{\text{–}}{a}=a=\text{constant}\text{.} [/latex]

Thus, we can use the symbol a for acceleration at all times. Assuming acceleration to be abiding does not seriously limit the situations we can study nor does information technology degrade the accuracy of our treatment. For i affair, acceleration is constant in a neat number of situations. Furthermore, in many other situations we can describe motion accurately by bold a constant dispatch equal to the average dispatch for that motility. Lastly, for motion during which acceleration changes drastically, such as a car accelerating to top speed and then braking to a cease, motion can exist considered in divide parts, each of which has its ain constant acceleration.

Displacement and Position from Velocity

To get our first two equations, we starting time with the definition of average velocity:

[latex] \overset{\text{–}}{v}=\frac{\text{Δ}x}{\text{Δ}t}. [/latex]

Substituting the simplified notation for [latex] \text{Δ}10 [/latex] and [latex] \text{Δ}t [/latex] yields

[latex] \overset{\text{–}}{five}=\frac{x-{x}_{0}}{t}. [/latex]

Solving for 10 gives us

[latex] ten={x}_{0}+\overset{\text{–}}{v}t, [/latex]

where the average velocity is

[latex] \overset{\text{–}}{v}=\frac{{five}_{0}+v}{2}. [/latex]

The equation [latex] \overset{\text{–}}{v}=\frac{{v}_{0}+five}{2} [/latex] reflects the fact that when dispatch is constant, v is but the simple average of the initial and final velocities. (Figure) illustrates this concept graphically. In role (a) of the effigy, dispatch is constant, with velocity increasing at a constant charge per unit. The boilerplate velocity during the ane-h interval from 40 km/h to 80 km/h is sixty km/h:

[latex] \overset{\text{–}}{five}=\frac{{five}_{0}+v}{2}=\frac{xl\,\text{km/h}+80\,\text{km/h}}{2}=60\,\text{km/h}\text{.} [/latex]

In office (b), acceleration is not constant. During the i-h interval, velocity is closer to eighty km/h than 40 km/h. Thus, the average velocity is greater than in part (a).

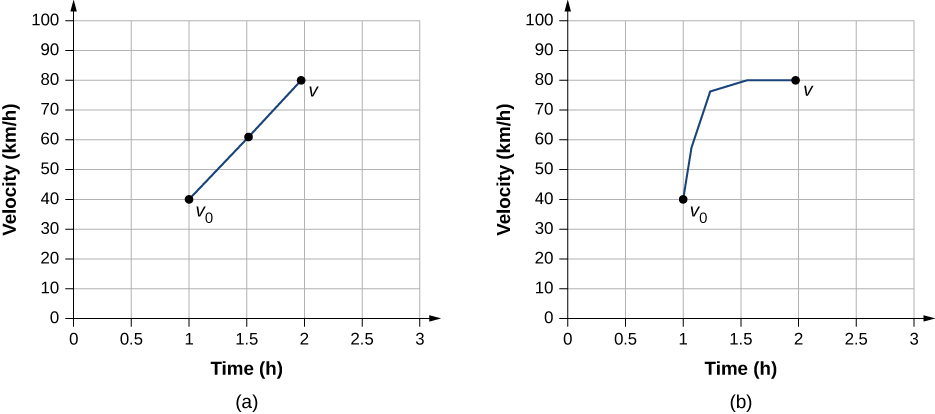
Figure 3.xviii (a) Velocity-versus-time graph with constant acceleration showing the initial and final velocities [latex] {v}_{0}\,\text{and}\,v [/latex]. The average velocity is [latex] \frac{1}{two}({v}_{0}+v)=60\,\text{km}\text{/}\text{h} [/latex]. (b) Velocity-versus-time graph with an dispatch that changes with fourth dimension. The average velocity is not given by [latex] \frac{1}{2}({v}_{0}+v) [/latex], but is greater than lx km/h.

Solving for Final Velocity from Acceleration and Time

We can derive another useful equation past manipulating the definition of acceleration:

[latex] a=\frac{\text{Δ}v}{\text{Δ}t}. [/latex]

Substituting the simplified notation for [latex] \text{Δ}v [/latex] and [latex] \text{Δ}t [/latex] gives us

[latex] a=\frac{v-{five}_{0}}{t}\enspace(\text{abiding}\,a). [/latex]

Solving for 5 yields

[latex] v={five}_{0}+at\enspace(\text{abiding}\,a). [/latex]

Example

Calculating Concluding Velocity

An airplane lands with an initial velocity of lxx.0 g/s then decelerates at ane.50 grand/s^two for twoscore.0 s. What is its last velocity?

Strategy

First, we place the knowns: [latex] {v}_{0}=70\,\text{m/s,}\,a=-ane.50{\,\text{1000/southward}}^{2},t=40\,\text{s} [/latex].

Second, we identify the unknown; in this instance, it is final velocity [latex] {five}_{\text{f}} [/latex].

Last, nosotros determine which equation to employ. To do this nosotros figure out which kinematic equation gives the unknown in terms of the knowns. We calculate the final velocity using (Figure), [latex] v={v}_{0}+at [/latex].

Solution

Figure 3.nineteen The airplane lands with an initial velocity of 70.0 m/s and slows to a final velocity of 10.0 m/southward earlier heading for the terminal. Annotation the acceleration is negative because its direction is opposite to its velocity, which is positive.

Significance

The final velocity is much less than the initial velocity, as desired when slowing down, but is still positive (see figure). With jet engines, reverse thrust tin can be maintained long enough to stop the plane and starting time moving it astern, which is indicated by a negative final velocity, but is not the case here.

In addition to being useful in problem solving, the equation [latex] five={v}_{0}+at [/latex] gives the states insight into the relationships among velocity, dispatch, and time. We can see, for example, that

• Concluding velocity depends on how large the dispatch is and how long it lasts
• If the acceleration is null, then the final velocity equals the initial velocity (v = five ₀), as expected (in other words, velocity is abiding)
• If a is negative, and then the concluding velocity is less than the initial velocity

All these observations fit our intuition. Notation that information technology is e'er useful to examine basic equations in light of our intuition and experience to check that they practice indeed describe nature accurately.

Solving for Terminal Position with Constant Acceleration

We can combine the previous equations to find a third equation that allows usa to calculate the final position of an object experiencing constant acceleration. We start with

[latex] v={five}_{0}+at. [/latex]

Adding [latex] {v}_{0} [/latex] to each side of this equation and dividing by 2 gives

[latex] \frac{{v}_{0}+v}{2}={v}_{0}+\frac{ane}{2}at. [/latex]

Since [latex] \frac{{v}_{0}+5}{ii}=\overset{\text{–}}{5} [/latex] for constant dispatch, we take

[latex] \overset{\text{–}}{v}={v}_{0}+\frac{i}{2}at. [/latex]

Now we substitute this expression for [latex] \overset{\text{–}}{v} [/latex] into the equation for displacement, [latex] x={x}_{0}+\overset{\text{–}}{v}t [/latex], yielding

[latex] 10={x}_{0}+{v}_{0}t+\frac{1}{2}a{t}^{two}\enspace(\text{constant}\,a). [/latex]

Instance

Calculating Displacement of an Accelerating Object

Dragsters can achieve an average dispatch of 26.0 m/sⁱⁱ. Suppose a dragster accelerates from rest at this charge per unit for 5.56 southward (Figure). How far does it travel in this time?

Effigy 3.20 U.S. Army Elevation Fuel pilot Tony "The Sarge" Schumacher begins a race with a controlled burnout. (credit: Lt. Col. William Thurmond. Photo Courtesy of U.Southward. Regular army.)

Strategy

First, let's draw a sketch (Effigy). We are asked to discover displacement, which is x if we have [latex] {x}_{0} [/latex] to exist zero. (Think virtually [latex] {10}_{0} [/latex] as the starting line of a race. It can be anywhere, but we call information technology goose egg and measure out all other positions relative to information technology.) Nosotros tin can apply the equation [latex] x={x}_{0}+{5}_{0}t+\frac{1}{two}a{t}^{2} [/latex] when we identify [latex] {five}_{0} [/latex], [latex] a [/latex], and t from the statement of the problem.

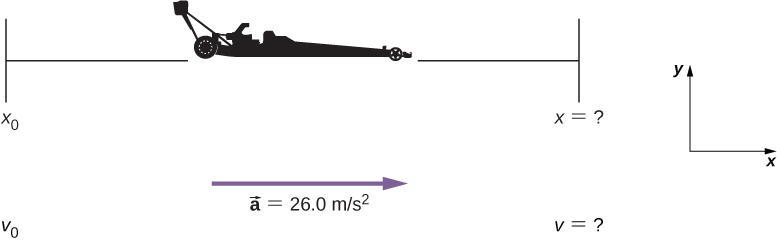
Figure 3.21 Sketch of an accelerating dragster.

Solution

Significance

If we convert 402 m to miles, nosotros discover that the distance covered is very close to one-quarter of a mile, the standard distance for drag racing. And then, our answer is reasonable. This is an impressive deportation to cover in only 5.56 s, but top-notch dragsters can do a quarter mile in fifty-fifty less fourth dimension than this. If the dragster were given an initial velocity, this would add another term to the distance equation. If the same acceleration and time are used in the equation, the distance covered would exist much greater.

What else can nosotros learn by examining the equation [latex] x={x}_{0}+{v}_{0}t+\frac{1}{2}a{t}^{two}? [/latex] We can run into the following relationships:

• Displacement depends on the square of the elapsed time when acceleration is not nada. In (Effigy), the dragster covers but ane-quaternary of the total distance in the first half of the elapsed time.
• If acceleration is naught, then initial velocity equals boilerplate velocity [latex] ({v}_{0}=\overset{\text{–}}{v}) [/latex], and [latex] x={ten}_{0}+{5}_{0}t+\frac{one}{2}\,a{t}^{2}\,\text{becomes}\,x={ten}_{0}+{v}_{0}t. [/latex]

Solving for Final Velocity from Distance and Dispatch

A fourth useful equation tin can be obtained from another algebraic manipulation of previous equations. If we solve [latex] v={5}_{0}+at [/latex] for t, we go

[latex] t=\frac{v-{five}_{0}}{a}. [/latex]

Substituting this and [latex] \overset{\text{–}}{v}=\frac{{v}_{0}+v}{ii} [/latex] into [latex] ten={10}_{0}+\overset{\text{–}}{v}t [/latex], nosotros become

[latex] {five}^{2}={v}_{0}^{two}+2a(ten-{x}_{0})\enspace(\text{constant}\,a). [/latex]

Example

Calculating Concluding Velocity

Calculate the last velocity of the dragster in (Figure) without using information about time.

Strategy

The equation [latex] {v}^{2}={v}_{0}^{2}+2a(x-{ten}_{0}) [/latex] is ideally suited to this task because information technology relates velocities, acceleration, and displacement, and no time data is required.

Solution

Significance

A velocity of 145 k/due south is well-nigh 522 km/h, or near 324 mi/h, only even this breakneck speed is short of the tape for the quarter mile. Too, note that a square root has two values; we took the positive value to betoken a velocity in the same direction as the dispatch.

An exam of the equation [latex] {5}^{two}={v}_{0}^{2}+2a(x-{ten}_{0}) [/latex] can produce additional insights into the general relationships among physical quantities:

• The final velocity depends on how big the dispatch is and the distance over which information technology acts.
• For a fixed acceleration, a automobile that is going twice as fast doesn't simply terminate in twice the altitude. Information technology takes much further to stop. (This is why we take reduced speed zones about schools.)

Putting Equations Together

In the following examples, nosotros go on to explore one-dimensional motion, only in situations requiring slightly more than algebraic manipulation. The examples also give insight into problem-solving techniques. The note that follows is provided for easy reference to the equations needed. Be aware that these equations are not independent. In many situations we have two unknowns and need two equations from the set to solve for the unknowns. We need as many equations equally there are unknowns to solve a given situation.

Summary of Kinematic Equations (constant a)

[latex] x={x}_{0}+\overset{\text{–}}{five}t [/latex]

[latex] \overset{\text{–}}{v}=\frac{{5}_{0}+v}{two} [/latex]

[latex] v={v}_{0}+at [/latex]

[latex] 10={x}_{0}+{v}_{0}t+\frac{i}{ii}a{t}^{2} [/latex]

[latex] {5}^{2}={five}_{0}^{two}+2a(x-{10}_{0}) [/latex]

Before we get into the examples, let'southward look at some of the equations more than closely to see the beliefs of acceleration at extreme values. Rearranging (Figure), we accept

[latex] a=\frac{five-{v}_{0}}{t}. [/latex]

From this we come across that, for a finite fourth dimension, if the divergence between the initial and concluding velocities is small, the acceleration is small, approaching zero in the limit that the initial and final velocities are equal. On the contrary, in the limit [latex] t\to 0 [/latex] for a finite difference between the initial and final velocities, acceleration becomes space.

Similarly, rearranging (Figure), nosotros can express acceleration in terms of velocities and displacement:

[latex] a=\frac{{5}^{2}-{v}_{0}^{2}}{2(x-{x}_{0})}. [/latex]

Thus, for a finite difference betwixt the initial and final velocities acceleration becomes infinite in the limit the displacement approaches naught. Acceleration approaches cypher in the limit the difference in initial and concluding velocities approaches nothing for a finite deportation.

Example

How Far Does a Auto Go?

On dry concrete, a car tin decelerate at a rate of 7.00 grand/s^two, whereas on moisture concrete it can decelerate at merely 5.00 1000/s². Notice the distances necessary to stop a car moving at 30.0 k/s (about 110 km/h) on (a) dry concrete and (b) wet concrete. (c) Repeat both calculations and detect the displacement from the indicate where the driver sees a traffic light turn cerise, taking into account his reaction fourth dimension of 0.500 southward to get his foot on the brake.

Strategy

First, we need to draw a sketch (Figure). To determine which equations are all-time to use, we need to list all the known values and identify exactly what we need to solve for.

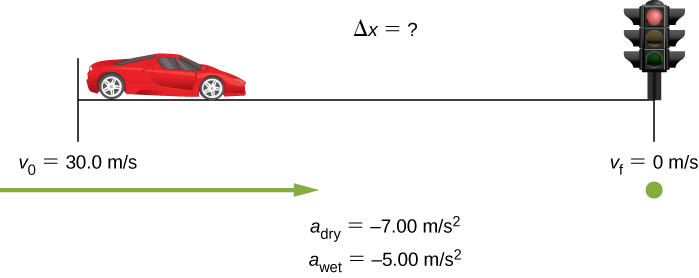
Figure 3.22 Sample sketch to visualize deceleration and stopping distance of a automobile.

Solution

1. Outset, we need to identify the knowns and what we want to solve for. We know that v ₀ = 30.0 chiliad/southward, v = 0, and a = −7.00 m/southward^two (a is negative because it is in a direction reverse to velocity). We take x ₀ to exist zero. We are looking for displacement [latex] \text{Δ}10 [/latex], or x − x ₀.Second, we identify the equation that will assist united states solve the problem. The best equation to use is

   [latex] {v}^{2}={v}_{0}^{two}+2a(x-{10}_{0}). [/latex]

   This equation is all-time considering information technology includes simply one unknown, x. Nosotros know the values of all the other variables in this equation. (Other equations would allow us to solve for x, but they require usa to know the stopping time, t, which we do non know. Nosotros could use them, but it would entail additional calculations.)

   Third, we rearrange the equation to solve for x:

   [latex] x-{10}_{0}=\frac{{five}^{two}-{v}_{0}^{ii}}{2a} [/latex]

   and substitute the known values:

   [latex] 10-0=\frac{{0}^{2}-{(thirty.0\,\text{m/s})}^{2}}{2(-7.00{\text{thou/southward}}^{2})}. [/latex]

   Thus,

   [latex] x=64.3\,\text{m on dry concrete}\text{.} [/latex]

2. This part can be solved in exactly the same style as (a). The only difference is that the dispatch is −5.00 m/southwardⁱⁱ. The result is

   [latex] {x}_{\text{moisture}}=90.0\,\text{thou on moisture concrete.} [/latex]

3. Show Respond

   When the driver reacts, the stopping distance is the aforementioned as it is in (a) and (b) for dry and wet concrete. So, to answer this question, nosotros need to calculate how far the car travels during the reaction fourth dimension, and then add that to the stopping fourth dimension. It is reasonable to presume the velocity remains constant during the driver's reaction time.To practice this, we, again, place the knowns and what we want to solve for. We know that [latex] \overset{\text{–}}{v}=30.0\,\text{m/s} [/latex], [latex] {t}_{\text{reaction}}=0.500\,\text{due south} [/latex], and [latex] {a}_{\text{reaction}}=0 [/latex]. We take [latex] {x}_{\text{0-reaction}} [/latex] to be zero. Nosotros are looking for [latex] {x}_{\text{reaction}} [/latex].Second, as before, we place the all-time equation to use. In this case, [latex] ten={x}_{0}+\overset{\text{–}}{5}t [/latex] works well because the only unknown value is x, which is what nosotros want to solve for.Third, we substitute the knowns to solve the equation: [latex] 10=0+(30.0\,\text{one thousand/southward})(0.500\,\text{s})=15.0\,\text{one thousand}. [/latex] This means the car travels 15.0 m while the driver reacts, making the total displacements in the 2 cases of dry out and wet concrete fifteen.0 one thousand greater than if he reacted instantly. Concluding, we then add the displacement during the reaction time to the displacement when braking ((Figure)), [latex] {10}_{\text{braking}}+{x}_{\text{reaction}}={x}_{\text{total}}, [/latex] and detect (a) to be 64.iii m + xv.0 m = 79.three thousand when dry and (b) to be 90.0 m + 15.0 m = 105 k when moisture.

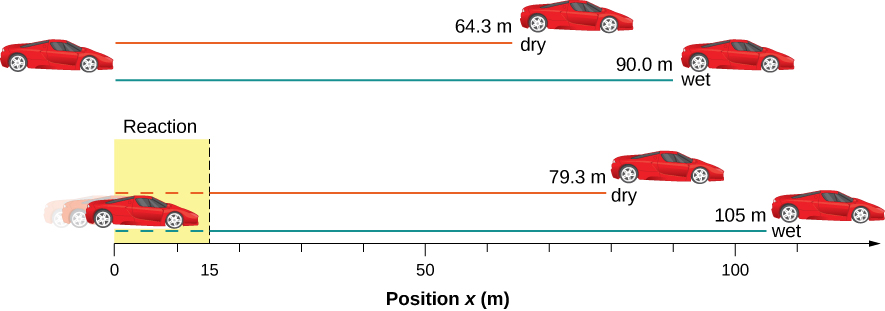
Effigy 3.23 The distance necessary to finish a car varies greatly, depending on road weather condition and commuter reaction time. Shown here are the braking distances for dry and moisture pavement, every bit calculated in this case, for a car traveling initially at xxx.0 k/s. Too shown are the total distances traveled from the point when the driver commencement sees a light plow red, assuming a 0.500-due south reaction time.

Significance

The displacements constitute in this example seem reasonable for stopping a fast-moving car. It should take longer to end a machine on moisture pavement than dry. It is interesting that reaction time adds significantly to the displacements, but more of import is the general approach to solving problems. We place the knowns and the quantities to be adamant, and then detect an appropriate equation. If there is more than than one unknown, we need as many independent equations as in that location are unknowns to solve. There is often more than one way to solve a problem. The various parts of this instance can, in fact, be solved by other methods, simply the solutions presented hither are the shortest.

Instance

Calculating Time

Suppose a car merges into expressway traffic on a 200-1000-long ramp. If its initial velocity is x.0 thousand/south and it accelerates at 2.00 m/southward², how long does it take the auto to travel the 200 k upwardly the ramp? (Such data might be useful to a traffic engineer.)

Strategy

Outset, we draw a sketch (Effigy). We are asked to solve for time t. Equally earlier, we identify the known quantities to choose a user-friendly physical relationship (that is, an equation with ane unknown, t.)

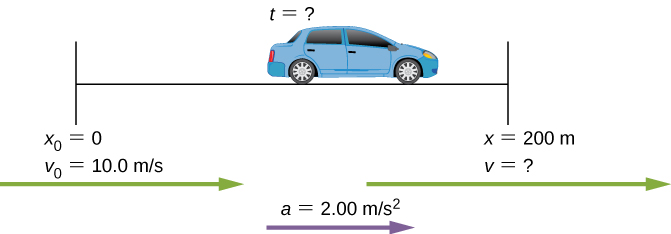
Figure 3.24 Sketch of a car accelerating on a freeway ramp.

Solution

Significance

Whenever an equation contains an unknown squared, in that location are two solutions. In some issues both solutions are meaningful; in others, only one solution is reasonable. The x.0-southward answer seems reasonable for a typical thruway on-ramp.

Check Your Agreement

A manned rocket accelerates at a charge per unit of 20 chiliad/south² during launch. How long does it accept the rocket to achieve a velocity of 400 m/due south?

Example

Acceleration of a Spaceship

A spaceship has left Globe's orbit and is on its style to the Moon. It accelerates at 20 g/southward² for 2 min and covers a distance of yard km. What are the initial and final velocities of the spaceship?

Strategy

We are asked to discover the initial and final velocities of the spaceship. Looking at the kinematic equations, we encounter that one equation will not give the reply. We must use one kinematic equation to solve for i of the velocities and substitute it into another kinematic equation to get the second velocity. Thus, we solve two of the kinematic equations simultaneously.

Solution

Significance

There are six variables in deportation, time, velocity, and acceleration that describe motion in i dimension. The initial conditions of a given problem can be many combinations of these variables. Because of this multifariousness, solutions may not exist like shooting fish in a barrel equally elementary substitutions into one of the equations. This example illustrates that solutions to kinematics may require solving two simultaneous kinematic equations.

With the nuts of kinematics established, nosotros tin can go on to many other interesting examples and applications. In the procedure of developing kinematics, nosotros have likewise glimpsed a general approach to problem solving that produces both correct answers and insights into concrete relationships. The next level of complication in our kinematics bug involves the motion of 2 interrelated bodies, called two-body pursuit problems.

Two-Body Pursuit Problems

Upwards until this signal we have looked at examples of movement involving a unmarried body. Even for the problem with two cars and the stopping distances on moisture and dry out roads, nosotros divided this problem into two separate problems to find the answers. In a two-body pursuit problem, the motions of the objects are coupled—significant, the unknown we seek depends on the motion of both objects. To solve these problems we write the equations of movement for each object and then solve them simultaneously to find the unknown. This is illustrated in (Figure).

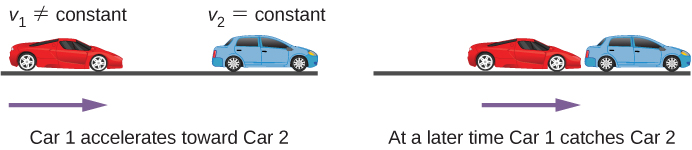
Effigy 3.25 A two-body pursuit scenario where car two has a constant velocity and car 1 is behind with a abiding acceleration. Machine one catches up with car ii at a later fourth dimension.

The time and distance required for car i to catch car ii depends on the initial distance car one is from auto ii equally well equally the velocities of both cars and the acceleration of car 1. The kinematic equations describing the motility of both cars must be solved to discover these unknowns.

Consider the following example.

Example

Cheetah Communicable a Gazelle

A cheetah waits in hiding backside a bush. The cheetah spots a gazelle running by at x grand/southward. At the instant the gazelle passes the cheetah, the cheetah accelerates from rest at 4 m/s² to grab the gazelle. (a) How long does information technology take the cheetah to take hold of the gazelle? (b) What is the displacement of the gazelle and cheetah?

Strategy

We use the prepare of equations for abiding dispatch to solve this problem. Since there are two objects in motility, we have separate equations of motion describing each animal. But what links the equations is a mutual parameter that has the same value for each animal. If we wait at the problem closely, information technology is clear the mutual parameter to each animal is their position 10 at a after fourth dimension t. Since they both kickoff at [latex] {x}_{0}=0 [/latex], their displacements are the same at a later time t, when the chetah catches up with the gazelle. If we pick the equation of motion that solves for the displacement for each animate being, we can then set the equations equal to each other and solve for the unknown, which is time.

Solution

1. Show Answer

   Equation for the gazelle: The gazelle has a constant velocity, which is its boilerplate velocity, since information technology is not accelerating. Therefore, nosotros utilise (Figure) with [latex] {x}_{0}=0 [/latex]: [latex] x={ten}_{0}+\overset{\text{–}}{v}t=\overset{\text{–}}{v}t. [/latex] Equation for the chetah: The cheetah is accelerating from residue, so nosotros use (Figure) with [latex] {10}_{0}=0 [/latex] and [latex] {v}_{0}=0 [/latex]: [latex] 10={x}_{0}+{v}_{0}t+\frac{1}{ii}a{t}^{2}=\frac{1}{2}a{t}^{2}. [/latex] Now we have an equation of motion for each animal with a common parameter, which tin exist eliminated to find the solution. In this case, we solve for t: [latex] \brainstorm{array}{cc} x=\overset{\text{–}}{v}t=\frac{one}{two}a{t}^{2}\hfill \\ t=\frac{2\overset{\text{–}}{v}}{a}.\hfill \end{assortment} [/latex] The gazelle has a constant velocity of 10 m/s, which is its average velocity. The acceleration of the cheetah is 4 m/s2. Evaluating t, the time for the cheetah to accomplish the gazelle, we have [latex] t=\frac{2\overset{\text{–}}{v}}{a}=\frac{two(x)}{4}=5\,\text{s}\text{.} [/latex]

2. Show Answer

   To go the displacement, we utilize either the equation of motion for the chetah or the gazelle, since they should both give the same respond.Displacement of the cheetah: [latex] ten=\frac{1}{2}a{t}^{2}=\frac{i}{ii}(iv){(5)}^{ii}=l\,\text{1000}\text{.} [/latex] Deportation of the gazelle: [latex] x=\overset{\text{–}}{v}t=ten(5)=l\,\text{m}\text{.} [/latex] Nosotros see that both displacements are equal, every bit expected.

Significance

It is important to clarify the motility of each object and to use the advisable kinematic equations to depict the private movement. It is likewise important to have a adept visual perspective of the two-torso pursuit trouble to encounter the common parameter that links the movement of both objects.

Check Your Agreement

A bicycle has a abiding velocity of ten thousand/southward. A person starts from balance and runs to grab up to the bike in 30 s. What is the acceleration of the person?

Show Solution

[latex] a=\frac{ii}{iii}{\,\text{g/s}}^{two} [/latex].

Summary

• When analyzing one-dimensional motion with constant acceleration, identify the known quantities and cull the advisable equations to solve for the unknowns. Either one or two of the kinematic equations are needed to solve for the unknowns, depending on the known and unknown quantities.
• Two-body pursuit problems ever require two equations to exist solved simultaneously for the unknowns.

Conceptual Questions

When analyzing the move of a single object, what is the required number of known physical variables that are needed to solve for the unknown quantities using the kinematic equations?

State 2 scenarios of the kinematics of unmarried object where 3 known quantities crave ii kinematic equations to solve for the unknowns.

Show Solution

If the acceleration, time, and displacement are the knowns, and the initial and final velocities are the unknowns, then ii kinematic equations must be solved simultaneously. Also if the final velocity, time, and displacement are the knowns then two kinematic equations must exist solved for the initial velocity and acceleration.

Bug

A particle moves in a straight line at a constant velocity of thirty m/due south. What is its displacement between t = 0 and t = v.0 s?

A particle moves in a straight line with an initial velocity of xxx m/due south and a constant acceleration of 30 m/s². If at [latex] t=0,10=0 [/latex] and [latex] v=0 [/latex], what is the particle's position at t = v s?

A particle moves in a direct line with an initial velocity of 30 m/s and constant acceleration 30 g/southward². (a) What is its displacement at t = 5 s? (b) What is its velocity at this aforementioned time?

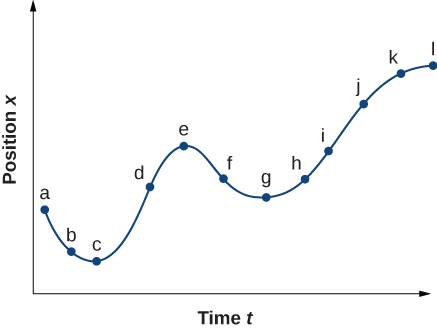
(a) Sketch a graph of velocity versus time respective to the graph of displacement versus time given in the post-obit figure. (b) Identify the time or times (t _a, t _b, t _c, etc.) at which the instantaneous velocity has the greatest positive value. (c) At which times is it nil? (d) At which times is information technology negative?

Testify Answer

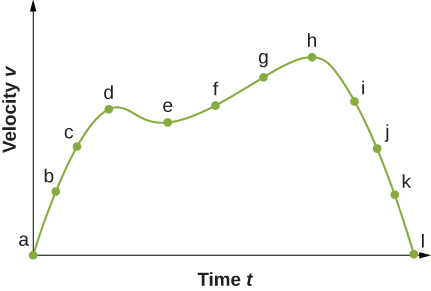
(a) Sketch a graph of acceleration versus fourth dimension respective to the graph of velocity versus time given in the following effigy. (b) Identify the time or times (t _a, t _b, t _c, etc.) at which the dispatch has the greatest positive value. (c) At which times is it zero? (d) At which times is it negative?

A particle has a constant acceleration of 6.0 m/sⁱⁱ. (a) If its initial velocity is 2.0 m/s, at what time is its displacement five.0 m? (b) What is its velocity at that time?

At t = x south, a particle is moving from left to right with a speed of v.0 thousand/south. At t = 20 s, the particle is moving right to left with a speed of 8.0 m/s. Assuming the particle's acceleration is constant, determine (a) its dispatch, (b) its initial velocity, and (c) the instant when its velocity is zilch.

A well-thrown ball is caught in a well-padded mitt. If the acceleration of the ball is[latex] 2.10\,×\,{10}^{4}{\,\text{m/southward}}^{two} [/latex], and 1.85 ms [latex] (1\,\text{ms}={10}^{-3}\,\text{s}) [/latex] elapses from the time the ball showtime touches the mitt until it stops, what is the initial velocity of the ball?

A bullet in a gun is accelerated from the firing sleeping accommodation to the terminate of the barrel at an boilerplate rate of [latex] 6.20\,×\,{10}^{five}{\,\text{m/s}}^{ii} [/latex] for [latex] 8.10\,×\,{10}^{\text{−}4}\,\text{s} [/latex]. What is its muzzle velocity (that is, its final velocity)?

Bear witness Solution

[latex] v=502.20\,\text{m/south} [/latex]

(a) A light-rail commuter train accelerates at a rate of 1.35 m/south^two. How long does it take to reach its meridian speed of 80.0 km/h, starting from rest? (b) The same train commonly decelerates at a charge per unit of ane.65 m/sⁱⁱ. How long does information technology have to come up to a stop from its peak speed? (c) In emergencies, the train tin decelerate more rapidly, coming to residuum from lxxx.0 km/h in 8.30 south. What is its emergency acceleration in meters per second squared?

While entering a throughway, a machine accelerates from residue at a rate of two.04 m/due southⁱⁱ for 12.0 s. (a) Draw a sketch of the state of affairs. (b) List the knowns in this trouble. (c) How far does the motorcar travel in those 12.0 s? To solve this part, offset identify the unknown, so betoken how yous chose the appropriate equation to solve for information technology. After choosing the equation, evidence your steps in solving for the unknown, check your units, and talk over whether the answer is reasonable. (d) What is the car'southward final velocity? Solve for this unknown in the same manner equally in (c), showing all steps explicitly.

Unreasonable results At the stop of a race, a runner decelerates from a velocity of 9.00 m/s at a rate of 2.00 m/s². (a) How far does she travel in the next 5.00 due south? (b) What is her final velocity? (c) Evaluate the event. Does it make sense?

Blood is accelerated from residuum to 30.0 cm/due south in a distance of 1.eighty cm by the left ventricle of the middle. (a) Brand a sketch of the state of affairs. (b) List the knowns in this problem. (c) How long does the dispatch take? To solve this role, beginning identify the unknown, then discuss how you lot chose the appropriate equation to solve for it. After choosing the equation, show your steps in solving for the unknown, checking your units. (d) Is the reply reasonable when compared with the time for a heartbeat?

During a slap shot, a hockey player accelerates the puck from a velocity of 8.00 m/s to 40.0 grand/due south in the same management. If this shot takes [latex] 3.33\,×\,{10}^{\text{−}2}\,\text{south} [/latex], what is the altitude over which the puck accelerates?

A powerful motorbike can accelerate from residuum to 26.8 k/due south (100 km/h) in only iii.90 southward. (a) What is its boilerplate acceleration? (b) How far does it travel in that time?

Evidence Solution

a. half dozen.87 s²; b. [latex] x=52.26\,\text{m} [/latex]

Freight trains can produce simply relatively small-scale accelerations. (a) What is the final velocity of a freight train that accelerates at a charge per unit of [latex] 0.0500\,{\text{k/south}}^{ii} [/latex] for 8.00 min, starting with an initial velocity of iv.00 m/s? (b) If the train can deadening down at a rate of [latex] 0.550\,{\text{m/s}}^{2} [/latex], how long will it take to come to a stop from this velocity? (c) How far volition information technology travel in each case?

A fireworks shell is accelerated from rest to a velocity of 65.0 m/s over a altitude of 0.250 yard. (a) Summate the acceleration. (b) How long did the acceleration last?

A swan on a lake gets airborne by flapping its wings and running on top of the water. (a) If the swan must accomplish a velocity of six.00 grand/s to have off and it accelerates from rest at an average rate of [latex] 0.35\,{\text{k/s}}^{2} [/latex], how far will it travel before becoming airborne? (b) How long does this take?

A woodpecker's brain is specially protected from large accelerations by tendon-like attachments inside the skull. While pecking on a tree, the woodpecker'southward head comes to a stop from an initial velocity of 0.600 yard/due south in a distance of only two.00 mm. (a) Find the acceleration in meters per second squared and in multiples of g, where k = nine.80 g/s². (b) Summate the stopping time. (c) The tendons cradling the brain stretch, making its stopping altitude 4.fifty mm (greater than the head and, hence, less acceleration of the brain). What is the encephalon'south acceleration, expressed in multiples of thousand?

An unwary football player collides with a padded goalpost while running at a velocity of 7.50 grand/s and comes to a full finish later on compressing the padding and his body 0.350 chiliad. (a) What is his acceleration? (b) How long does the standoff last?

A care package is dropped out of a cargo plane and lands in the woods. If nosotros assume the care bundle speed on touch on is 54 m/s (123 mph), then what is its dispatch? Presume the copse and snowfall stops information technology over a distance of 3.0 1000.

Show Solution

Knowns: [latex] x=iii\,\text{thousand,}\,v=0\,\text{1000/s,}\enspace{v}_{0}=54\,\text{m/south} [/latex]. We desire a, and then we can use this equation: [latex] a=\text{−}486\,{\text{g/due south}}^{2} [/latex].

An express railroad train passes through a station. Information technology enters with an initial velocity of 22.0 yard/south and decelerates at a rate of [latex] 0.150\,{\text{m/due south}}^{2} [/latex] as it goes through. The station is 210.0 m long. (a) How fast is information technology going when the nose leaves the station? (b) How long is the olfactory organ of the train in the station? (c) If the railroad train is 130 m long, what is the velocity of the end of the train as information technology leaves? (d) When does the stop of the railroad train leave the station?

Unreasonable results Dragsters can actually reach a meridian speed of 145.0 m/due south in only 4.45 south. (a) Calculate the boilerplate acceleration for such a dragster. (b) Find the final velocity of this dragster starting from rest and accelerating at the rate found in (a) for 402.0 k (a quarter mile) without using whatsoever information on time. (c) Why is the last velocity greater than that used to discover the average acceleration? (Hint: Consider whether the assumption of constant acceleration is valid for a dragster. If not, discuss whether the dispatch would be greater at the beginning or cease of the run and what effect that would accept on the final velocity.)

Glossary

two-body pursuit problem

a kinematics problem in which the unknowns are calculated by solving the kinematic equations simultaneously for two moving objects

goodridgetwout1977.blogspot.com

Source: https://courses.lumenlearning.com/suny-osuniversityphysics/chapter/3-4-motion-with-constant-acceleration/

Share this post